تويت
الرسالة الثانية
الموسومة بجومطريا في الهندسة وبيان ماهيتها
بسم الله الرحمن الرحيم
الْحَمْدُ لِلهِ وَسَلَامٌ عَلَى عِبَادِهِ الَّذِينَ اصْطَفَى آللهُ خَيْرٌ أَمَّا يُشْرِكُونَ
اعلم أيها الأخ البار الرحيم، أيدك الله وإيانا بروح منه، أنَّا قد فرغنا من رسالة العدد في الأرثماطيقي، وبينا من خواص العدد قدر الكفاية والجهد، وانتقلنا من تلك الرسالة إلى هذه الرسالة التي هي الثانيةُ من رسالة الرياضيات في المدخل إلى علم الهندسة، فنقول:
اعلم بأن العلوم التي كان القدماء يخرجون أولادهم بها ويروضون بها تلامذتهم أربعة أجناس، أولها العلوم الرياضيات، والثاني العلوم المنطقيات، والثالث العلوم الطبيعيات، والرابعُ العلومُ الإلهيات، فالرياضياتُ أربعةُ أنواع، أولها الأثماطيقي وهو معرفة العدد وكمية أجناسه وخواصه وأنواعه وخواص تلك الأنواع، ومبدأ هذا العلم من الواحد الذي قبل الاثنين، والثاني «الجومطريا» وهو علم الهندسة وهي معرفةُ المقادير والأبعاد وكمية أنواعها وخواص تلك الأنواع ومبدأ هذا العلم من النقطة التي هي طرف الخط؛ أي نهايته، والثالث الأسطرنوميا يعني: علم النجوم، وهو معرفةُ تركيب الأفلاك وتخطيط البُرُوج وعدد الكواكب وطبائعها ودلائلها على الأشياء الكائنات في هذا العلم من حركة الشمس، والرابع الموسيقى وهو معرفةُ التأليفات والنسب بين الأشياء المختلفة والجواهر المتضادة القوى، ومبدأ هذا العلم من نسبة المساواة نسبة الثلاثة إلى الستة كنسبة الاثنين إلى الأربعة.
وأما المنطقيات فهي معرفةُ معاني الأشياء الموجودة التي هي مصورةٌ في أفكار النفوس ومبدأها من الجوهر، وأما الطبيعيات فهي معرفة جواهر الأجسام وما يَعرض لها من الأعراض، ومبدأ هذا العلم من الحركة والسكون، وأما الإلهيات فهي معرفةُ الصورة المجردة المفارقة للهيولى، ومبدأ هذا العلم من معرفة جوهر النفس كالملائكة والنفوس والشياطين والجن والأرواح بلا أجسام، وأن الأجسام عندهم ذوو أبعاد ثلاثة، ومبدأ هذا العلم من جوهر النفس.
وقد عملنا في كل نوع من هذه العلوم رسالة شبه المدخل والمقدمات، فأولها رسالة في العدد قبل هذه، وقد بينا فيها طرفًا من خواص الأعداد وكمية أنواعها وكيفية نشوئها من الواحد الذي قبل الاثنين، ونريد أن نُبين ونذكر في هذه الرسالة أصل الهندسة التي هي أصلُ المقادير الثلاثة وكمية أنواعها وخواص تلك الأنواع وكيفية نشوئها من النقطة التي هي رأس الخط وأنها في صناعة الهندسة مثل الواحد في صناعة العدد.
واعلمْ أيها الأخ البار الرحيم، أيدك الله وإيانا بروح منه، أن الهندسة يُقال على نوعين عقليةٌ وحسيةٌ، فالحسيةُ هي معرفةُ المقادير وما يعرض فيها من المعاني إذا أُضيف بعضها إلى بعض، وهي ما يُرى بالبصر ويُدرك باللمس، والعقلي بضد ذلك، وهو ما يُعرف ويفهم، فالذي يُرى بالبصر هو الخط والسطح والجسم ذوو الأبعاد وما يعرض فيها، كما أن الثقل في الثقيل لا يعرف إلا بالعقل والثقل عينُ الثقيل، والمقادير ثلاثة أنواع وهي الخطوط والسطوح والأجسام، وهذه الهندسة تدخل في الصنائع كلها، وذلك أن كل صانع إذا قدر في صناعته قبل العمل فهو ضربٌ من الهندسة العقلية فهي معرفة الأبعاد وما يعرض فيها من المعاني إذا أضيف بعضها إلى بعض وهي ما يتصور في النفس بالفكر، وهي ثلاثة أنواع الطول والعرض والعمق، وهذه الأبعاد العقلية صفاتٌ لتلك المقادير الحسية، وذلك أَنَّ الخط هو أحدُ المقادير وله صفةٌ واحدةٌ، وهي الطولُ حسب، وأما السطح فهو مقدار ثانٍ وله صفتان وهما الطول والعرض، وأما الجسم فهو مقدار ثالث وله ثلاث صفات وهي الطول والعرض والعمق.
واعلمْ أن النظر في هذه الأبعاد مجردة عن الأجسام من صناعة المحققين فنبدأ أولًا بوصف الهندسة الحسية؛ لأنها أقربُ إلى فهم المتعلمين، فنقول:
إن الخط الحسي الذي هو أحد المقادير أصله النقطة كَمَا بَيَّنَّا قبل في الرسالة التي في خواص العدد بأن الواحد أصل العدد؛ وذلك أن النقطة الحسية إذا انتظمت ظهر الخط بحاسة النظر مثل هذا ••••• فإنا لا نقول: إن هذه النقطةَ شيء لا جزء له، لكن النقطة العقلية هي لا جزء لها، ونقول أيضًا: الخط أصل السطح كما أن النقطة أصل الخط، وكما أن الواحد أصل الاثنين، والاثنان أصل لعدد الزوج — كَمَا بَيَّنَّا قبل ذلك — وذلك أن الخطوط إذا تجاورتْ ظهر السطح لحاسة البصر مثل هذا
ونقول: إن السطح أصل للجسم كما أن الخط أصل للسطح والنقطة أصل للخط كما أن الواحد أصل الاثنين والاثنان والواحد أصلان لأول الفرد — كَمَا بَيَّنَّا قبل ذلك — وذلك أن السطوح إذا تراكمت بعضُها فوق بعض ظهر الجسم لحاسة النظر مثل هذا 
.
(١) فصل في أنواع الخط
فنقول: الخطوط ثلاثة أنواع أولها المستقيم وهو مثل الذي يخط بالمسطر على ما يرى في هذه الصورة مثل هذا ─── والثاني المقوس وهو مثل الذي يخط بالبركار
مثل هذا والثالث الخط المنحني وهو المركب منهما مثل هذا 
فهذه أنواع الخطوط الثلاثة.
(٢) فصل في ألقاب الخطوط المستقيمة
فنقول: إن الخطوط المستقيمة إذا أضيف بعضها إلى بعض إما أن تكون متساوية أو متوازية أو متلاقية أو متماسة أو متقاطعة، فالمتساوية هي التي طولها واحد مثال هذا
والمتوازية هي التي إذا كانت في سطح واحد وأخرجت في كلتي الجهتين إخراجًا دائمًا لا يلتقيان أبدًا مثل هذا 
والمتلاقية هي التي تلتقي في إحدى الجهتين وتحيط بزاوية واحدة مثل هذا 
والمتماسة هي التي تماس إحداهما الأخرى وتحدث زاويتين أو زاوية مثل هذا المثال 
والمتقاطعة التي تقطع إحداهما الأخرى وتحدث من تقاطعهما أربع زوايا مثل هذا 
فهذه ألقاب الخطوط المستقيمة.
(٣) فصل في أسماء الخط المستقيم
إذا قام خط مستقيم على خط آخر قيامًا مستويًا من غير ميل إلى طرف يقال عند ذلك للخط القائم العمود وللقائم عليه القاعدة مثل هذا
، وإذا أضيف الخطان إلى زاوية يقال لهما: الساقان لتلك الزاوية مثل هذا 
.
وإذا قام خط مستقيم على خط وللخط والقائم ميل إلى أحد الطرفين يحصل زاويتان إحداهما أكبر يقال لها: المنفرجة والأخرى أصغر يقال لها: الحادة، وكل خط مستقيم يقابل زاوية ما يقال له: وتر تلك الزاوية التي يقابلها مثل هذا
والخطوط إذا أضيفت إلى سطح ما يقال لها: أضلاع ذلك السطح مثل هذا 
وكل خط يخرج من زاوية وينتهي إلى أخرى يقال له: قطر المربع مثل هذا 
وكل خط يخرج من زاوية المثلث وينتهي إلى الضلع المقابل لها ويقوم على الخط المقابل لها على زاويا قائمة يقال لذلك الخط: مسقط الحجر، ويقال له: العمود أيضًا، ويقال للخط الذي وقع عليه مسقط الحجر القاعدة مثل هذا 
فهذه أسماء الخطوط المستقيمة.
(٤) فصل في أنواع الزوايا
نقول: إن الزوايا على نوعين مسطح ومجسم، والمسطحة هي التي يحيط بها خطان على غير استقامة مثل هذا
والمجسمة هي التي تحيط بها ثلاثة خطوط في زاوية كل اثنين زاوية على غير استقامة.
(٥) فصل في أنواع الزوايا المسطحة
تتنوع من جهة الخطوط ثلاثة أنواع إما من خطين مستقيمين مثل هذا
أو خطين مقوسين مثل هذا 
أو أحدهما مقوس والآخر مستقيم، والزوايا التي تحيط بها خطوط مستقيمة تتنوع من جهة الكيفية ثلاثة أنواع: قائمة ومنفرجة وحادة، فالقائمة هي التي إذا قام خط مستقيم على خط آخر مستقيم قيامًا مستويًا حدث عن جنبيه زاويتان متساويتان وكل واحدة منهما يقال لها: زاوية قائمة مثل هذا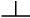 
، وإذا قام ذلك الخط قيامًا غير مستوٍ على خط مستقيم حدث عن جنبيه زاويتان مختلفتان إحداهما أكبر من القائمة يقال لها: المنفرجة والأخرى أصغر من القائمة يقال لها: الحادة ومجموعهما مساوٍ لقائمتين؛ لأن الزاوية الحادة تنقض عن القائمة بمقدار زيادة المنفرجة على القائمة على هذا المثال 
فهذا عدد أنواع الزوايا.
(٦) فصل في أنواع الخطوط القوسية
فنقول: إن الخطوط القوسية أربعة أنواع منها محيط الدائرة، ومنها نصف الدائرة، ومنها أكثر من نصف الدائرة، ومنها أقل من نصف الدائرة، ومركز الدائرة هي النقطة التي في وسط الدائرة، وقطر الدائرة هو الخط المستقيم الذي يقطع الدائرة بنصفين، والوتر الخط المستقيم الذي يصل بين طرفي الخط المقوس، والسهم هو الخط المستقيم الذي يفصل الوتر والقوس كل واحد منهما بنصفين، وهو إذا أضيف إلى نصف القوس يقال له عند ذلك: الجيب المعكوس وإذا أضيف نصف الوتر إلى نصف القوس يقال له عند ذلك: الجيب المستوي والخطوط المقوسة المتوازية هي التي مركزها واحد مثل هذا
.
والخطوط القوسية المتقاطعة هي التي مراكزها مختلفة مثل هذا:
والخطوط القوسية المتماسة هي التي تماس بعضها بعضًا إما من داخل أو خارج ولا يتقاطع مثل هذا 
وأما الخطوط المنحنية فقد تركنا ذكرها لأنها غير مستعملة، فاعلم جميع ذلك.
(٧) فصل في ذكر السطوح
فنقول: السطح هو شكلٌ يحيطُ به الخط أو خطوط، والدائرة هي شكل يحيط به خط واحد مثل هذا
وفي داخله نقطة كل الخطوط المستقيمة التي تخرج منها وينتهي إلى جهتين مساوٍ بعضهما لبعض، ونصف الدائرة شكل يحيط به خطان أحدهما مقوس والآخر مستقيم مثل هذا 
وقطعة الدائرة هو شكل يحيط به خط مستقيم وقوس من محيط الدائرة إما أكبر من نصفه وإما أصغر حسب ما بينا وأوردنا مثالها قبل هذا.
(٨) فصل في الأشكال المستقيمة الخطوط وأنواعها
فنقول: الأشكال التي يحيط بها خطوط مستقيمة أولها الشكل المثلث وهو الذي يحيط به ثلاثة خطوط وله ثلاث زوايا مثل هذا
، ثم المربع وهو الذي يحيط به أربعة خطوط مستقيمة وأربع زوايا قائمات مثل هذا 
، ثم المخمس وهو شكل يحيط به خمسة خطوط وله خمس زوايا مثل هذا 
، ثم المسدس وهو الذي يحيط به ستة خطوط وله ست زوايا مثل هذا 
، وبعده المسبع مثل هذا 
، وعلى هذا القياس تتزايد الأشكال كتزايد العدد.
فصل
وقد بينا أن الخطوط يظهر طولها لحاسة البصر من النقطة إذا انتظمت فأقصر خط من نقطتين مثل هذا •• ثم من ثلاث مثل هذا ••• ثم من أربع مثل هذا •••• ثم من خمس مثل هذا ••••• ويتزايد واحدًا بعد واحد كتزايد العدد على النظم الطبيعي، وأصغر شكل المثلث من ثلاثة أجزاء مثل هذا
ثم من أربعة أجزاء مثل هذا 
ثم من عشرة أجزاء مثل هذا 
.
وعلى هذا القياس يتزايد كما يتزايد جمع العدد على النظم الطبيعي، وأما الأشكال المربعات فأولها تظهر في أربعة أجزاء مثل هذا
وبعده من تسعة أجزاء مثل هذا 
وبعده من ستة عشر مثل هذا 
وبعده من خمسة وعشرين جزءًا مثل هذا 
.
وعلى هذا القياس تتزايد المربعات دائمًا كتزايد جمع العدد على نظم طبيعة الأفراد وتكون كلها مجذورات.
(٩) فصل في بيان المثلث أنه أصل لجميع الأشكال
فنقول: إن الشكل المثلث أصل لجميع الأشكال المستقيمة الخطوط كما أن الواحد أصل لجميع العدد، والنقطة أصل للخطوط، والخط أصل للسطوح، والسطح أصل للأجسام كما بينا قبل، وذلك أنه إذا أضيف شكل مثلث إلى شكل آخر مثله حدث من جملتهما شكل مربع مثل هذا
وإذا أضيف إليهما شكل آخر مثلث حدث من ذلك شكل مخمس، وإن أضيف إليها شكل آخر مثلث حدث شكل مسدس وإن أضيف إليها شكل آخر حدث من ذلك شكل مسبع مثل هذا 
وعلى هذا القياس تحدث الأشكال المستقيمة الخطوط الكثيرة الزوايا من الشكل المثلث إذا ضم بعضها إلى بعض وتتزايد دائمًا بلا نهاية كتزايد العدد من الآحاد إذا ضم بعضها إلى بعض دائمًا بلا نهاية كما بيَّنا قبل.
وقد تبين أن من الشكل المثلث تتركب الأشكال المستقيمة الخطوط، وأن من السطح تتركب الأجسام، وأن من الخطوط تتركب السطوح، وأن من النقطة تتركب الخطوط، كما أن من الواحد يتركب العدد، فإن النقطة في صناعة الهندسة كالواحد في صناعة العدد وكما أن الواحد لا جزء له فكذلك النقطة العقلية لا جزء لها.
(١٠) فصل في أنواع السطوح
السطوح من جهة الكيفية تتنوع ثلاثة أنواع: مسطحًا ومقعرًا ومقببًا، فالمسطح كوجوه الألواح والمقعر كقعر الأواني والمقبب كظهر القباب، ومن الأشكال ما يسمى البيضي مثل هذا
ومنها الهلالي مثل هذا 
ومنها المخروط الصنوبري مثل هذا 
ومنها الإهليلجي 
ومنها نيم خانجي مثل هذا 
ومنها الطبلي مثل هذا 
ومنها الزيتوني مثل هذا 
.
(١١) فصل في ذكر الأجسام
فنقول: السطوح هي نهايات الأجسام ونهايات السطوح الخطوط ونهايات الخطوط هي النقط، وذلك أن كل خط لا بد أن يبتدئ من نقطة وينتهي إلى أخرى، فكل سطح ينتهي إلى خط أو خطوط وكل جسم فلا بد من أن ينتهي إلى سطح أو سطوح، فمن الأجسام ما يحيط به سطح واحد وهي الكرة ومنها ما يحيط به سطحان وهو نصف الكرة، وذلك أن سطحًا منه مقبب وسطحًا مدور، ومن الأجسام ما يحيط به ثلاثة سطوح وهو ربع الكرة، ومنها ما يحيط به أربعة سطوح مثلثات ويسمى الشكل الناري، ومنها ما يحيط به خمسة سطوح ومنها ما يحيط به ستة سطوح مربعات فمنها المكعب ومنها اللبني ومنها البئري ومنها اللوحي، فالجسم المكعب هو الذي طوله مثل عرضه وعرضه مثل سمكه وله ستة سطوح مربعات متساوية الأضلاع قائمة الزوايا وله ثماني زوايا مجسمة وأربع وعشرون زاوية مسطحة واثنا عشر ضلعًا متساوية كل أربعة منها متوازية، وهذه صورتها:
.
وأما الجسم البئري فهو الذي طوله مثل عرضه وسمكه أكبر منهما وله ستة سطوح مربعات، اثنان منهما متقابلان متساويا الأضلاع، قائما الزوايا، وأربعة ضيقات مستطيلات متساوية الأضلاع قائمة الزوايا، وله اثنا عشر ضلعًا أربعة منها طوال متساوية متوازية وثمانية قصار متساوية متوازية وله ثماني زوايا مجسمة وأربع عشرون زاوية مسطحة:
.
وأما الجسم اللوحي فهو الذي طوله أكبر من عرضه وعرضه أكبر من سمكه وله ستة سطوح مربعات اثنان منها طويلان متقابلان متسعان ومتساويَا الأضلاع قائمَا الزوايا وسطحان آخران قصيران ضيقان متساويا الأضلاع قائما الزوايا وله اثنا عشر ضلعًا أربعة منها طوالٌ وأربعة منها قصار وأربعة أقصرُ من ذلك وله ثماني زوايا مجسمة وأربع وعشرون زاوية مسطحة مثل هذا:
.
وأما الجسم اللبني فهو الذي طوله مثل عرضه وسمكه أقل منهما وله ستة سطوح مربعات، اثنان منها واسعان متقابلان متساويَا الأضلاع قائمَا الزوايا وأربعة منها ضيقات مستطيلات متساوية الأضلاع قائمة الزوايا وله اثنا عشر ضلعًا أربعة منها قصار متساوية متوازية وثمانية منها طوال متساوية كل أربعة منها متوازية ولها ثماني زوايا مجسمات وأربع وعشرون زاوية مسطحة مثل هذا
.
وأما الجسم الكري فهو الذي يحيط به سطح واحد وفي داخله نقطة وكل الخطوط المستقيمة الخارجة من تلك النقطة إلى سطح الكرة متساوية يقال لتلك النقطة: مركز الدائرة، وإذا دارت الكرة فيكون في سطحها نقطتان متقابلتان ساكنتان يقال لهما: قطب الكرة مثل هذا
.
وإذا وصل بينهما بخط مستقيم جاز ذلك الخط على مركز الكرة يقال له: محور الكرة، وإذا اتصل الخط من نقطة إلى نقطة فهو المحور.
وإذْ قد ذكرنا طرفًا من أصل الهندسة الحسية شبه المدخل والمقدمات، وقلنا: إن هذا العلم يحتاج إليه أكثر الصناع فلنبينْ ذلك، وهو التقدير قبل العمل؛ لأن كل صانع يؤلف الأجسامَ بعضها إلى بعض ويُرَكِّبُها فلا بد له أن يقدر أولًا المكان في أي موضع يعملها والزمان في أي وقت يعملها ويبتدئ فيها والإمكان هل يقدر عليه أم لا وبأي آلة وأدوات يعملها وكيف يؤلف أجزاءها حتى تلتئم وتأتلف، فهذه هي الهندسة التي تدخل في أكثر الصنائع التي هي تأليفُ الأجسام بعضها إلى بعض.
واعلمْ أن كثيرًا من الحيوانات تعمل صنعة طبيعية قد جُبلت عليها بلا تعليم كالنحل في اتخاذها البيوت، وذلك أنها تبني بيوتها مطبقات مستديرات الشكل كالأتراس بعضها فوق بعض وتجعل ثقب البيوت كلها مسدسات الأضلاع والزوايا لما في ذلك من إتقان الحكمة؛ لأن من خَاصِّيَّة هذا الشكل أنه أوسع من المربع والمخمس وأنها تكشف تلك الثقوب حتى لا يكون بينها خلل فيدخل الهواء فتفسد العسل فيعفن، وهذا مثال ذلك:
.
وهكذا العنكبوت تنسج شبكتها في زاويا البيت والحائط شفقة عليها من تخريق الرياح وتمزيق حملها، وأما كيفية نسجها فهو أن تمد سداها على الاستقامة وخيوط لحمتها على الاستدارة؛ لما فيه من سهولة العمل، وهذا مثال ذلك:
.
ومن الناس من يستخرج صناعة بقريحته وذكاء نفسه لم يسبق إليها، وأما أكثر الصناع فإنهم يأخذونها توقيفًا وتعليمًا من الأستاذين.
فصل
واعلم يا أخي أيدك الله وإيانا بروح منه؛ أن علم الهندسة يدخل في الصنائع كلها وخاصة في المساحة وهي صناعة يحتاج إليها العمال والكتاب والدهاقين وأصحاب الضياع والعقارات في معاملاتهم من جباية الخراج وحفر الأنهار وعمل البريدات وما شاكلها.
ثم اعلم بأن المقادير التي تمسح بها الأراضي بالعراق خمسة مقادير، وهي الأشل والباب والذراع والقبضة والأصبع، واعلمْ بأن الأصبع الواحدة غلظها ست شعيرات مصفوفة مضمومة ظهور بعضها إلى بطون بعض والقبضة الواحدة أربع أصابع والذراع الواحدة ثماني قبضات، وهو اثنان وثلاثون أصبعًا والباب طولُهُ ست أذرع وهي ثمانٍ وأربعون قبضة وهو مائة واثنان وتسعون أصبعًا والأشل حبل طوله عشرة أبواب وهو ستون ذراعًا وأربعمائة وثمانون قبضة وألف وتسعمائة وعشرون أصبعًا.
واعلم بأنك إذا ضربت هذه المقادير بعضها في بعض، فالذي يخرج منها يسمى تكسيرًا، فإذا جمعت فيكون منها جريبات وقفيزات وعشيرات، وأما حسابها فهو أن القبضة الواحدة في مثلها تكون ستة عشر أصبعًا والذراع الواحدة في مثلها تكون أربعًا وستين قبضة مكسرة وألفًا وأربعة وعشرين أصبعًا مكسرة وهو تسع ربع عشر عشير الجريب والباب الواحد في مثله يكون ستًّا وثلاثين ذراعًا مكسرة، وهذه صورتُها ٣٦ وهو ٢٣٠٤ قبضات مكسرة وهو ٣٦٨٦٤ أصبعًا مكسرة، وهو عشر عشير الجريب.
وأما الأشل في مثله فيكونُ جريبًا وهو عشرةُ أقفزة وهو مائة عشير، وهذه صورتُها ٣٦٠٠ ذراع مكسرة وهو ٢٣٠٤٠٠ قبضة مكسرة وهو ٣٦٨٦٤٠٠ أصبعًا مكسرة، وأما القفيزُ فهو عشرةُ أعشار وهو عشرة أبواب مكسرة، وهو مِن ضرب تسعة عشر ذراعًا إلا شيئًا يسيرًا في مثله وهو ثلاثمائة وستون ذراعًا، وأما العشير فهو من ضرب باب واحد في مثله وهو ٣٦ ذراعًا مكسرة وهو ٢٣٠٤ قبضات مكسرة وهو ٣٦٨٦٤ أصبعًا مكسرة، والأشوال في الأشوال واحدها جريب وعشرتها عشرة أجربة، والأشوال في الأبواب واحدها قفيز وعشرتها جريب، والأشوال في الأذرع واحدها عشير وثلثا عشير وست منها قفيز، والأشل في القبضات واحدها سدس عشير وربع سدس عشير وكل ثلاثة أخماس منها عشير، وكل ٣٦ منها قفيز والأشل في الأصابع كل واحد منها ربع سدس عشير وربع ربع سدس عشير وكل عشرة منها ربعا عشير وسدس ثمن عشير.
والأبواب في الأبواب واحدها عشيرٌ وعشرتُها قفيزٌ والأبوابُ في الأذرع واحدها سدس عشير وستة منها عشير، والأبواب في القبضات كل واحد منها ثلاثة أرباع ربع تسع عشير، والأبواب في الأصابع كل خمسة وثمانين منها ثلث عشير وربع سدس عشير وتسع عشير تقريبًا، وكل أربعة منها ثلاثة أرباع وتسع عشير وكل مائة ثمان وعشرين منها ثلثا ثلث عشير والأذرع في الأذرع واحدها ربع تسع عشير، وكل أربع منها تسع عشير وكل مائة منها عشيران وثلثا عشير وتسع عشير.
فهذا شرح مساحة العرض والطول، فأما مساحةُ العُمق فهو أن تضرب الطول في العرض فما اجتمع من ذلك فاضربْه في العمق وما يجتمع فهو تكسيرُ المجسم والحاجة إلى هذا العمل عند حفر الأنهار والآبار والحفائر والبريدات والمسنيات والأساسات للديار والبنيان، وما شاكل ذلك.
ثم اعلمْ يا أخي، أيدك الله وإيانا بروح منه، أنه قد تدخل الشبه في كل صناعة علمية على مَن يتعاطاها وليس من أهلها وكان ناقصًا فيها أو ساهيًا عنها، مثال ذلك ما ذكروا أن رجلًا باع من رجل آخرَ قطعة أرض بألف درهم على أن طولها مائة ذراع وعرضها مائة ذراع، ثم قال له: خذ مني عوضًا عنها قطعتين من أرض كل واحدة منهما طولها خمسون ذراعًا وعرضها خمسون ذراعًا، وتوهم أن ذلك حقه فتحًا كما إلى قاض غير مهندس فقضى بمثل ذلك خطأ ثم تحاكما إلى حاكم من أهل الصناعة فحكم بأن ذلك نصف حقه، وهكذا أيضًا ذكر أن رجلًا استأجر رجلًا على أن يحفر له بركة طولها أربع أذرع في عرض أربع أذرع في عمق أربع أذرع بثمانية دراهم، فحفر له ذراعين في ذراعين طولًا وعرضًا وعمقًا، فطالبه بأربعة دراهم نصف الأجرة فتنازعا وتحاكما إلى مفتٍ غير مهندس، فحكم بأن ذلك حقه ثم تحاكما إلى أهل الصناعة فحكموا له بدرهم واحد، وقيل لرجل يتعاطى الحساب ولم يكن من أهله: كم نسبة ألف ألف إلى ألف ألف ألف؟ فقال: ثلثان، فقال أهل الصناعة: إنه عشر عشر العشر، فعلى هذا المثال تدخل الشبهة على كل من يتعاطى صناعة وليس من أهلها ومن أجل هذا قيل: استعينوا على كل صنعة بأهلها.
الموسومة بجومطريا في الهندسة وبيان ماهيتها
بسم الله الرحمن الرحيم
الْحَمْدُ لِلهِ وَسَلَامٌ عَلَى عِبَادِهِ الَّذِينَ اصْطَفَى آللهُ خَيْرٌ أَمَّا يُشْرِكُونَ
اعلم أيها الأخ البار الرحيم، أيدك الله وإيانا بروح منه، أنَّا قد فرغنا من رسالة العدد في الأرثماطيقي، وبينا من خواص العدد قدر الكفاية والجهد، وانتقلنا من تلك الرسالة إلى هذه الرسالة التي هي الثانيةُ من رسالة الرياضيات في المدخل إلى علم الهندسة، فنقول:
اعلم بأن العلوم التي كان القدماء يخرجون أولادهم بها ويروضون بها تلامذتهم أربعة أجناس، أولها العلوم الرياضيات، والثاني العلوم المنطقيات، والثالث العلوم الطبيعيات، والرابعُ العلومُ الإلهيات، فالرياضياتُ أربعةُ أنواع، أولها الأثماطيقي وهو معرفة العدد وكمية أجناسه وخواصه وأنواعه وخواص تلك الأنواع، ومبدأ هذا العلم من الواحد الذي قبل الاثنين، والثاني «الجومطريا» وهو علم الهندسة وهي معرفةُ المقادير والأبعاد وكمية أنواعها وخواص تلك الأنواع ومبدأ هذا العلم من النقطة التي هي طرف الخط؛ أي نهايته، والثالث الأسطرنوميا يعني: علم النجوم، وهو معرفةُ تركيب الأفلاك وتخطيط البُرُوج وعدد الكواكب وطبائعها ودلائلها على الأشياء الكائنات في هذا العلم من حركة الشمس، والرابع الموسيقى وهو معرفةُ التأليفات والنسب بين الأشياء المختلفة والجواهر المتضادة القوى، ومبدأ هذا العلم من نسبة المساواة نسبة الثلاثة إلى الستة كنسبة الاثنين إلى الأربعة.
وأما المنطقيات فهي معرفةُ معاني الأشياء الموجودة التي هي مصورةٌ في أفكار النفوس ومبدأها من الجوهر، وأما الطبيعيات فهي معرفة جواهر الأجسام وما يَعرض لها من الأعراض، ومبدأ هذا العلم من الحركة والسكون، وأما الإلهيات فهي معرفةُ الصورة المجردة المفارقة للهيولى، ومبدأ هذا العلم من معرفة جوهر النفس كالملائكة والنفوس والشياطين والجن والأرواح بلا أجسام، وأن الأجسام عندهم ذوو أبعاد ثلاثة، ومبدأ هذا العلم من جوهر النفس.
وقد عملنا في كل نوع من هذه العلوم رسالة شبه المدخل والمقدمات، فأولها رسالة في العدد قبل هذه، وقد بينا فيها طرفًا من خواص الأعداد وكمية أنواعها وكيفية نشوئها من الواحد الذي قبل الاثنين، ونريد أن نُبين ونذكر في هذه الرسالة أصل الهندسة التي هي أصلُ المقادير الثلاثة وكمية أنواعها وخواص تلك الأنواع وكيفية نشوئها من النقطة التي هي رأس الخط وأنها في صناعة الهندسة مثل الواحد في صناعة العدد.
واعلمْ أيها الأخ البار الرحيم، أيدك الله وإيانا بروح منه، أن الهندسة يُقال على نوعين عقليةٌ وحسيةٌ، فالحسيةُ هي معرفةُ المقادير وما يعرض فيها من المعاني إذا أُضيف بعضها إلى بعض، وهي ما يُرى بالبصر ويُدرك باللمس، والعقلي بضد ذلك، وهو ما يُعرف ويفهم، فالذي يُرى بالبصر هو الخط والسطح والجسم ذوو الأبعاد وما يعرض فيها، كما أن الثقل في الثقيل لا يعرف إلا بالعقل والثقل عينُ الثقيل، والمقادير ثلاثة أنواع وهي الخطوط والسطوح والأجسام، وهذه الهندسة تدخل في الصنائع كلها، وذلك أن كل صانع إذا قدر في صناعته قبل العمل فهو ضربٌ من الهندسة العقلية فهي معرفة الأبعاد وما يعرض فيها من المعاني إذا أضيف بعضها إلى بعض وهي ما يتصور في النفس بالفكر، وهي ثلاثة أنواع الطول والعرض والعمق، وهذه الأبعاد العقلية صفاتٌ لتلك المقادير الحسية، وذلك أَنَّ الخط هو أحدُ المقادير وله صفةٌ واحدةٌ، وهي الطولُ حسب، وأما السطح فهو مقدار ثانٍ وله صفتان وهما الطول والعرض، وأما الجسم فهو مقدار ثالث وله ثلاث صفات وهي الطول والعرض والعمق.
واعلمْ أن النظر في هذه الأبعاد مجردة عن الأجسام من صناعة المحققين فنبدأ أولًا بوصف الهندسة الحسية؛ لأنها أقربُ إلى فهم المتعلمين، فنقول:
إن الخط الحسي الذي هو أحد المقادير أصله النقطة كَمَا بَيَّنَّا قبل في الرسالة التي في خواص العدد بأن الواحد أصل العدد؛ وذلك أن النقطة الحسية إذا انتظمت ظهر الخط بحاسة النظر مثل هذا ••••• فإنا لا نقول: إن هذه النقطةَ شيء لا جزء له، لكن النقطة العقلية هي لا جزء لها، ونقول أيضًا: الخط أصل السطح كما أن النقطة أصل الخط، وكما أن الواحد أصل الاثنين، والاثنان أصل لعدد الزوج — كَمَا بَيَّنَّا قبل ذلك — وذلك أن الخطوط إذا تجاورتْ ظهر السطح لحاسة البصر مثل هذا
ونقول: إن السطح أصل للجسم كما أن الخط أصل للسطح والنقطة أصل للخط كما أن الواحد أصل الاثنين والاثنان والواحد أصلان لأول الفرد — كَمَا بَيَّنَّا قبل ذلك — وذلك أن السطوح إذا تراكمت بعضُها فوق بعض ظهر الجسم لحاسة النظر مثل هذا .(١) فصل في أنواع الخط
فنقول: الخطوط ثلاثة أنواع أولها المستقيم وهو مثل الذي يخط بالمسطر على ما يرى في هذه الصورة مثل هذا ─── والثاني المقوس وهو مثل الذي يخط بالبركار
مثل هذا والثالث الخط المنحني وهو المركب منهما مثل هذا فهذه أنواع الخطوط الثلاثة.(٢) فصل في ألقاب الخطوط المستقيمة
فنقول: إن الخطوط المستقيمة إذا أضيف بعضها إلى بعض إما أن تكون متساوية أو متوازية أو متلاقية أو متماسة أو متقاطعة، فالمتساوية هي التي طولها واحد مثال هذا
والمتوازية هي التي إذا كانت في سطح واحد وأخرجت في كلتي الجهتين إخراجًا دائمًا لا يلتقيان أبدًا مثل هذا والمتلاقية هي التي تلتقي في إحدى الجهتين وتحيط بزاوية واحدة مثل هذا والمتماسة هي التي تماس إحداهما الأخرى وتحدث زاويتين أو زاوية مثل هذا المثال والمتقاطعة التي تقطع إحداهما الأخرى وتحدث من تقاطعهما أربع زوايا مثل هذا فهذه ألقاب الخطوط المستقيمة.(٣) فصل في أسماء الخط المستقيم
إذا قام خط مستقيم على خط آخر قيامًا مستويًا من غير ميل إلى طرف يقال عند ذلك للخط القائم العمود وللقائم عليه القاعدة مثل هذا
، وإذا أضيف الخطان إلى زاوية يقال لهما: الساقان لتلك الزاوية مثل هذا .وإذا قام خط مستقيم على خط وللخط والقائم ميل إلى أحد الطرفين يحصل زاويتان إحداهما أكبر يقال لها: المنفرجة والأخرى أصغر يقال لها: الحادة، وكل خط مستقيم يقابل زاوية ما يقال له: وتر تلك الزاوية التي يقابلها مثل هذا
والخطوط إذا أضيفت إلى سطح ما يقال لها: أضلاع ذلك السطح مثل هذا وكل خط يخرج من زاوية وينتهي إلى أخرى يقال له: قطر المربع مثل هذا وكل خط يخرج من زاوية المثلث وينتهي إلى الضلع المقابل لها ويقوم على الخط المقابل لها على زاويا قائمة يقال لذلك الخط: مسقط الحجر، ويقال له: العمود أيضًا، ويقال للخط الذي وقع عليه مسقط الحجر القاعدة مثل هذا فهذه أسماء الخطوط المستقيمة.(٤) فصل في أنواع الزوايا
نقول: إن الزوايا على نوعين مسطح ومجسم، والمسطحة هي التي يحيط بها خطان على غير استقامة مثل هذا
والمجسمة هي التي تحيط بها ثلاثة خطوط في زاوية كل اثنين زاوية على غير استقامة.(٥) فصل في أنواع الزوايا المسطحة
تتنوع من جهة الخطوط ثلاثة أنواع إما من خطين مستقيمين مثل هذا
أو خطين مقوسين مثل هذا أو أحدهما مقوس والآخر مستقيم، والزوايا التي تحيط بها خطوط مستقيمة تتنوع من جهة الكيفية ثلاثة أنواع: قائمة ومنفرجة وحادة، فالقائمة هي التي إذا قام خط مستقيم على خط آخر مستقيم قيامًا مستويًا حدث عن جنبيه زاويتان متساويتان وكل واحدة منهما يقال لها: زاوية قائمة مثل هذا 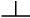، وإذا قام ذلك الخط قيامًا غير مستوٍ على خط مستقيم حدث عن جنبيه زاويتان مختلفتان إحداهما أكبر من القائمة يقال لها: المنفرجة والأخرى أصغر من القائمة يقال لها: الحادة ومجموعهما مساوٍ لقائمتين؛ لأن الزاوية الحادة تنقض عن القائمة بمقدار زيادة المنفرجة على القائمة على هذا المثال فهذا عدد أنواع الزوايا.(٦) فصل في أنواع الخطوط القوسية
فنقول: إن الخطوط القوسية أربعة أنواع منها محيط الدائرة، ومنها نصف الدائرة، ومنها أكثر من نصف الدائرة، ومنها أقل من نصف الدائرة، ومركز الدائرة هي النقطة التي في وسط الدائرة، وقطر الدائرة هو الخط المستقيم الذي يقطع الدائرة بنصفين، والوتر الخط المستقيم الذي يصل بين طرفي الخط المقوس، والسهم هو الخط المستقيم الذي يفصل الوتر والقوس كل واحد منهما بنصفين، وهو إذا أضيف إلى نصف القوس يقال له عند ذلك: الجيب المعكوس وإذا أضيف نصف الوتر إلى نصف القوس يقال له عند ذلك: الجيب المستوي والخطوط المقوسة المتوازية هي التي مركزها واحد مثل هذا
.والخطوط القوسية المتقاطعة هي التي مراكزها مختلفة مثل هذا:
والخطوط القوسية المتماسة هي التي تماس بعضها بعضًا إما من داخل أو خارج ولا يتقاطع مثل هذا وأما الخطوط المنحنية فقد تركنا ذكرها لأنها غير مستعملة، فاعلم جميع ذلك.(٧) فصل في ذكر السطوح
فنقول: السطح هو شكلٌ يحيطُ به الخط أو خطوط، والدائرة هي شكل يحيط به خط واحد مثل هذا
وفي داخله نقطة كل الخطوط المستقيمة التي تخرج منها وينتهي إلى جهتين مساوٍ بعضهما لبعض، ونصف الدائرة شكل يحيط به خطان أحدهما مقوس والآخر مستقيم مثل هذا وقطعة الدائرة هو شكل يحيط به خط مستقيم وقوس من محيط الدائرة إما أكبر من نصفه وإما أصغر حسب ما بينا وأوردنا مثالها قبل هذا.(٨) فصل في الأشكال المستقيمة الخطوط وأنواعها
فنقول: الأشكال التي يحيط بها خطوط مستقيمة أولها الشكل المثلث وهو الذي يحيط به ثلاثة خطوط وله ثلاث زوايا مثل هذا
، ثم المربع وهو الذي يحيط به أربعة خطوط مستقيمة وأربع زوايا قائمات مثل هذا ، ثم المخمس وهو شكل يحيط به خمسة خطوط وله خمس زوايا مثل هذا ، ثم المسدس وهو الذي يحيط به ستة خطوط وله ست زوايا مثل هذا ، وبعده المسبع مثل هذا ، وعلى هذا القياس تتزايد الأشكال كتزايد العدد.فصل
وقد بينا أن الخطوط يظهر طولها لحاسة البصر من النقطة إذا انتظمت فأقصر خط من نقطتين مثل هذا •• ثم من ثلاث مثل هذا ••• ثم من أربع مثل هذا •••• ثم من خمس مثل هذا ••••• ويتزايد واحدًا بعد واحد كتزايد العدد على النظم الطبيعي، وأصغر شكل المثلث من ثلاثة أجزاء مثل هذا
ثم من أربعة أجزاء مثل هذا ثم من عشرة أجزاء مثل هذا .وعلى هذا القياس يتزايد كما يتزايد جمع العدد على النظم الطبيعي، وأما الأشكال المربعات فأولها تظهر في أربعة أجزاء مثل هذا
وبعده من تسعة أجزاء مثل هذا وبعده من ستة عشر مثل هذا وبعده من خمسة وعشرين جزءًا مثل هذا .وعلى هذا القياس تتزايد المربعات دائمًا كتزايد جمع العدد على نظم طبيعة الأفراد وتكون كلها مجذورات.
(٩) فصل في بيان المثلث أنه أصل لجميع الأشكال
فنقول: إن الشكل المثلث أصل لجميع الأشكال المستقيمة الخطوط كما أن الواحد أصل لجميع العدد، والنقطة أصل للخطوط، والخط أصل للسطوح، والسطح أصل للأجسام كما بينا قبل، وذلك أنه إذا أضيف شكل مثلث إلى شكل آخر مثله حدث من جملتهما شكل مربع مثل هذا
وإذا أضيف إليهما شكل آخر مثلث حدث من ذلك شكل مخمس، وإن أضيف إليها شكل آخر مثلث حدث شكل مسدس وإن أضيف إليها شكل آخر حدث من ذلك شكل مسبع مثل هذا وعلى هذا القياس تحدث الأشكال المستقيمة الخطوط الكثيرة الزوايا من الشكل المثلث إذا ضم بعضها إلى بعض وتتزايد دائمًا بلا نهاية كتزايد العدد من الآحاد إذا ضم بعضها إلى بعض دائمًا بلا نهاية كما بيَّنا قبل.وقد تبين أن من الشكل المثلث تتركب الأشكال المستقيمة الخطوط، وأن من السطح تتركب الأجسام، وأن من الخطوط تتركب السطوح، وأن من النقطة تتركب الخطوط، كما أن من الواحد يتركب العدد، فإن النقطة في صناعة الهندسة كالواحد في صناعة العدد وكما أن الواحد لا جزء له فكذلك النقطة العقلية لا جزء لها.
(١٠) فصل في أنواع السطوح
السطوح من جهة الكيفية تتنوع ثلاثة أنواع: مسطحًا ومقعرًا ومقببًا، فالمسطح كوجوه الألواح والمقعر كقعر الأواني والمقبب كظهر القباب، ومن الأشكال ما يسمى البيضي مثل هذا
ومنها الهلالي مثل هذا ومنها المخروط الصنوبري مثل هذا ومنها الإهليلجي ومنها نيم خانجي مثل هذا ومنها الطبلي مثل هذا ومنها الزيتوني مثل هذا .(١١) فصل في ذكر الأجسام
فنقول: السطوح هي نهايات الأجسام ونهايات السطوح الخطوط ونهايات الخطوط هي النقط، وذلك أن كل خط لا بد أن يبتدئ من نقطة وينتهي إلى أخرى، فكل سطح ينتهي إلى خط أو خطوط وكل جسم فلا بد من أن ينتهي إلى سطح أو سطوح، فمن الأجسام ما يحيط به سطح واحد وهي الكرة ومنها ما يحيط به سطحان وهو نصف الكرة، وذلك أن سطحًا منه مقبب وسطحًا مدور، ومن الأجسام ما يحيط به ثلاثة سطوح وهو ربع الكرة، ومنها ما يحيط به أربعة سطوح مثلثات ويسمى الشكل الناري، ومنها ما يحيط به خمسة سطوح ومنها ما يحيط به ستة سطوح مربعات فمنها المكعب ومنها اللبني ومنها البئري ومنها اللوحي، فالجسم المكعب هو الذي طوله مثل عرضه وعرضه مثل سمكه وله ستة سطوح مربعات متساوية الأضلاع قائمة الزوايا وله ثماني زوايا مجسمة وأربع وعشرون زاوية مسطحة واثنا عشر ضلعًا متساوية كل أربعة منها متوازية، وهذه صورتها:
.وأما الجسم البئري فهو الذي طوله مثل عرضه وسمكه أكبر منهما وله ستة سطوح مربعات، اثنان منهما متقابلان متساويا الأضلاع، قائما الزوايا، وأربعة ضيقات مستطيلات متساوية الأضلاع قائمة الزوايا، وله اثنا عشر ضلعًا أربعة منها طوال متساوية متوازية وثمانية قصار متساوية متوازية وله ثماني زوايا مجسمة وأربع عشرون زاوية مسطحة:
.وأما الجسم اللوحي فهو الذي طوله أكبر من عرضه وعرضه أكبر من سمكه وله ستة سطوح مربعات اثنان منها طويلان متقابلان متسعان ومتساويَا الأضلاع قائمَا الزوايا وسطحان آخران قصيران ضيقان متساويا الأضلاع قائما الزوايا وله اثنا عشر ضلعًا أربعة منها طوالٌ وأربعة منها قصار وأربعة أقصرُ من ذلك وله ثماني زوايا مجسمة وأربع وعشرون زاوية مسطحة مثل هذا:
.وأما الجسم اللبني فهو الذي طوله مثل عرضه وسمكه أقل منهما وله ستة سطوح مربعات، اثنان منها واسعان متقابلان متساويَا الأضلاع قائمَا الزوايا وأربعة منها ضيقات مستطيلات متساوية الأضلاع قائمة الزوايا وله اثنا عشر ضلعًا أربعة منها قصار متساوية متوازية وثمانية منها طوال متساوية كل أربعة منها متوازية ولها ثماني زوايا مجسمات وأربع وعشرون زاوية مسطحة مثل هذا
.وأما الجسم الكري فهو الذي يحيط به سطح واحد وفي داخله نقطة وكل الخطوط المستقيمة الخارجة من تلك النقطة إلى سطح الكرة متساوية يقال لتلك النقطة: مركز الدائرة، وإذا دارت الكرة فيكون في سطحها نقطتان متقابلتان ساكنتان يقال لهما: قطب الكرة مثل هذا
.وإذا وصل بينهما بخط مستقيم جاز ذلك الخط على مركز الكرة يقال له: محور الكرة، وإذا اتصل الخط من نقطة إلى نقطة فهو المحور.
وإذْ قد ذكرنا طرفًا من أصل الهندسة الحسية شبه المدخل والمقدمات، وقلنا: إن هذا العلم يحتاج إليه أكثر الصناع فلنبينْ ذلك، وهو التقدير قبل العمل؛ لأن كل صانع يؤلف الأجسامَ بعضها إلى بعض ويُرَكِّبُها فلا بد له أن يقدر أولًا المكان في أي موضع يعملها والزمان في أي وقت يعملها ويبتدئ فيها والإمكان هل يقدر عليه أم لا وبأي آلة وأدوات يعملها وكيف يؤلف أجزاءها حتى تلتئم وتأتلف، فهذه هي الهندسة التي تدخل في أكثر الصنائع التي هي تأليفُ الأجسام بعضها إلى بعض.
واعلمْ أن كثيرًا من الحيوانات تعمل صنعة طبيعية قد جُبلت عليها بلا تعليم كالنحل في اتخاذها البيوت، وذلك أنها تبني بيوتها مطبقات مستديرات الشكل كالأتراس بعضها فوق بعض وتجعل ثقب البيوت كلها مسدسات الأضلاع والزوايا لما في ذلك من إتقان الحكمة؛ لأن من خَاصِّيَّة هذا الشكل أنه أوسع من المربع والمخمس وأنها تكشف تلك الثقوب حتى لا يكون بينها خلل فيدخل الهواء فتفسد العسل فيعفن، وهذا مثال ذلك:
.وهكذا العنكبوت تنسج شبكتها في زاويا البيت والحائط شفقة عليها من تخريق الرياح وتمزيق حملها، وأما كيفية نسجها فهو أن تمد سداها على الاستقامة وخيوط لحمتها على الاستدارة؛ لما فيه من سهولة العمل، وهذا مثال ذلك:
.ومن الناس من يستخرج صناعة بقريحته وذكاء نفسه لم يسبق إليها، وأما أكثر الصناع فإنهم يأخذونها توقيفًا وتعليمًا من الأستاذين.
فصل
واعلم يا أخي أيدك الله وإيانا بروح منه؛ أن علم الهندسة يدخل في الصنائع كلها وخاصة في المساحة وهي صناعة يحتاج إليها العمال والكتاب والدهاقين وأصحاب الضياع والعقارات في معاملاتهم من جباية الخراج وحفر الأنهار وعمل البريدات وما شاكلها.
ثم اعلم بأن المقادير التي تمسح بها الأراضي بالعراق خمسة مقادير، وهي الأشل والباب والذراع والقبضة والأصبع، واعلمْ بأن الأصبع الواحدة غلظها ست شعيرات مصفوفة مضمومة ظهور بعضها إلى بطون بعض والقبضة الواحدة أربع أصابع والذراع الواحدة ثماني قبضات، وهو اثنان وثلاثون أصبعًا والباب طولُهُ ست أذرع وهي ثمانٍ وأربعون قبضة وهو مائة واثنان وتسعون أصبعًا والأشل حبل طوله عشرة أبواب وهو ستون ذراعًا وأربعمائة وثمانون قبضة وألف وتسعمائة وعشرون أصبعًا.
واعلم بأنك إذا ضربت هذه المقادير بعضها في بعض، فالذي يخرج منها يسمى تكسيرًا، فإذا جمعت فيكون منها جريبات وقفيزات وعشيرات، وأما حسابها فهو أن القبضة الواحدة في مثلها تكون ستة عشر أصبعًا والذراع الواحدة في مثلها تكون أربعًا وستين قبضة مكسرة وألفًا وأربعة وعشرين أصبعًا مكسرة وهو تسع ربع عشر عشير الجريب والباب الواحد في مثله يكون ستًّا وثلاثين ذراعًا مكسرة، وهذه صورتُها ٣٦ وهو ٢٣٠٤ قبضات مكسرة وهو ٣٦٨٦٤ أصبعًا مكسرة، وهو عشر عشير الجريب.
وأما الأشل في مثله فيكونُ جريبًا وهو عشرةُ أقفزة وهو مائة عشير، وهذه صورتُها ٣٦٠٠ ذراع مكسرة وهو ٢٣٠٤٠٠ قبضة مكسرة وهو ٣٦٨٦٤٠٠ أصبعًا مكسرة، وأما القفيزُ فهو عشرةُ أعشار وهو عشرة أبواب مكسرة، وهو مِن ضرب تسعة عشر ذراعًا إلا شيئًا يسيرًا في مثله وهو ثلاثمائة وستون ذراعًا، وأما العشير فهو من ضرب باب واحد في مثله وهو ٣٦ ذراعًا مكسرة وهو ٢٣٠٤ قبضات مكسرة وهو ٣٦٨٦٤ أصبعًا مكسرة، والأشوال في الأشوال واحدها جريب وعشرتها عشرة أجربة، والأشوال في الأبواب واحدها قفيز وعشرتها جريب، والأشوال في الأذرع واحدها عشير وثلثا عشير وست منها قفيز، والأشل في القبضات واحدها سدس عشير وربع سدس عشير وكل ثلاثة أخماس منها عشير، وكل ٣٦ منها قفيز والأشل في الأصابع كل واحد منها ربع سدس عشير وربع ربع سدس عشير وكل عشرة منها ربعا عشير وسدس ثمن عشير.
والأبواب في الأبواب واحدها عشيرٌ وعشرتُها قفيزٌ والأبوابُ في الأذرع واحدها سدس عشير وستة منها عشير، والأبواب في القبضات كل واحد منها ثلاثة أرباع ربع تسع عشير، والأبواب في الأصابع كل خمسة وثمانين منها ثلث عشير وربع سدس عشير وتسع عشير تقريبًا، وكل أربعة منها ثلاثة أرباع وتسع عشير وكل مائة ثمان وعشرين منها ثلثا ثلث عشير والأذرع في الأذرع واحدها ربع تسع عشير، وكل أربع منها تسع عشير وكل مائة منها عشيران وثلثا عشير وتسع عشير.
فهذا شرح مساحة العرض والطول، فأما مساحةُ العُمق فهو أن تضرب الطول في العرض فما اجتمع من ذلك فاضربْه في العمق وما يجتمع فهو تكسيرُ المجسم والحاجة إلى هذا العمل عند حفر الأنهار والآبار والحفائر والبريدات والمسنيات والأساسات للديار والبنيان، وما شاكل ذلك.
ثم اعلمْ يا أخي، أيدك الله وإيانا بروح منه، أنه قد تدخل الشبه في كل صناعة علمية على مَن يتعاطاها وليس من أهلها وكان ناقصًا فيها أو ساهيًا عنها، مثال ذلك ما ذكروا أن رجلًا باع من رجل آخرَ قطعة أرض بألف درهم على أن طولها مائة ذراع وعرضها مائة ذراع، ثم قال له: خذ مني عوضًا عنها قطعتين من أرض كل واحدة منهما طولها خمسون ذراعًا وعرضها خمسون ذراعًا، وتوهم أن ذلك حقه فتحًا كما إلى قاض غير مهندس فقضى بمثل ذلك خطأ ثم تحاكما إلى حاكم من أهل الصناعة فحكم بأن ذلك نصف حقه، وهكذا أيضًا ذكر أن رجلًا استأجر رجلًا على أن يحفر له بركة طولها أربع أذرع في عرض أربع أذرع في عمق أربع أذرع بثمانية دراهم، فحفر له ذراعين في ذراعين طولًا وعرضًا وعمقًا، فطالبه بأربعة دراهم نصف الأجرة فتنازعا وتحاكما إلى مفتٍ غير مهندس، فحكم بأن ذلك حقه ثم تحاكما إلى أهل الصناعة فحكموا له بدرهم واحد، وقيل لرجل يتعاطى الحساب ولم يكن من أهله: كم نسبة ألف ألف إلى ألف ألف ألف؟ فقال: ثلثان، فقال أهل الصناعة: إنه عشر عشر العشر، فعلى هذا المثال تدخل الشبهة على كل من يتعاطى صناعة وليس من أهلها ومن أجل هذا قيل: استعينوا على كل صنعة بأهلها.
، والثاني الحاد الزوايا المتساوي الضلعين مثل هذا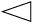 
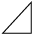
تعليق